Five color theorem
The five color theorem is a result from graph theory that given a plane separated into regions, such as a political map of the counties of a state, the regions may be colored using no more than five colors in such a way that no two adjacent regions receive the same color.
The five color theorem is implied by the stronger four color theorem, but is considerably easier to prove. It was based on a failed attempt at the four color proof by Alfred Kempe in 1879. Percy John Heawood found an error 11 years later, and proved the five color theorem based on Kempe's work. The four color theorem was finally proven by Kenneth Appel and Wolfgang Haken at the University of Illinois, with the aid of a computer. They were assisted in some algorithmic work by John A. Koch.
Contents |
Outline of the proof by contradiction
First of all, one associates a planar graph  to the given map, namely one puts a vertex in each region of the map, then connects two vertices with an edge if and only if the corresponding regions share a common border. The problem is then translated into a graph coloring problem: one has to paint the vertices of the graph so that no edge has endpoints of the same color.
to the given map, namely one puts a vertex in each region of the map, then connects two vertices with an edge if and only if the corresponding regions share a common border. The problem is then translated into a graph coloring problem: one has to paint the vertices of the graph so that no edge has endpoints of the same color.
The proof relies on the Euler characteristic to show that there must be a vertex  shared by at most five edges, and on the fact that
shared by at most five edges, and on the fact that  is planar, i.e. it may be embedded in the plane without intersecting edges.
is planar, i.e. it may be embedded in the plane without intersecting edges.
Now remove  from
from  . The graph
. The graph 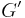 obtained this way has one fewer vertex than
obtained this way has one fewer vertex than  , so we can assume by induction that it can be colored with only five colors.
, so we can assume by induction that it can be colored with only five colors.  must be connected to five other vertices, since if not it can be colored in
must be connected to five other vertices, since if not it can be colored in  with a color not used by them. So now look at those five vertices
with a color not used by them. So now look at those five vertices 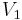 ,
, 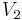 ,
, 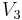 ,
, 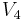 ,
, 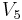 that were adjacent to
that were adjacent to  in cyclic order (which depends on how we write G). If we did not use all the five colors on them, then obviously we can paint
in cyclic order (which depends on how we write G). If we did not use all the five colors on them, then obviously we can paint  in a consistent way to render our graph 5-colored.
in a consistent way to render our graph 5-colored.
So we can assume that 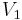 ,
, 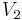 ,
, 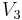 ,
, 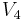 ,
, 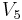 are colored with colors 1, 2, 3, 4, 5 respectively.
are colored with colors 1, 2, 3, 4, 5 respectively.
Now consider the subgraph 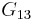 of
of 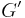 consisting of the vertices that are colored with colors 1 and 3 only, and edges connecting two of them. If
consisting of the vertices that are colored with colors 1 and 3 only, and edges connecting two of them. If 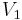 and
and 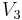 lie in different connected components of
lie in different connected components of 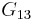 , we can reverse the coloration on that containing
, we can reverse the coloration on that containing 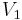 , thus assigning color number 1 to
, thus assigning color number 1 to  and completing the task.
and completing the task.
If on the contrary 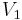 and
and 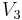 lie in the same connected component of
lie in the same connected component of 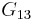 , we can find a path in
, we can find a path in 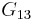 joining them, that is a sequence of edges and vertices painted only with colors 1 and 3.
joining them, that is a sequence of edges and vertices painted only with colors 1 and 3.
Now turn to the subgraph 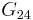 of
of 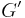 consisting of the vertices that are colored with colors 2 and 4 only, and edges connecting two of them, and apply the same arguments as before. Then either we are able to reverse a coloration on a subgraph of
consisting of the vertices that are colored with colors 2 and 4 only, and edges connecting two of them, and apply the same arguments as before. Then either we are able to reverse a coloration on a subgraph of 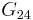 and paint
and paint  with, say, color number 2, or we can connect
with, say, color number 2, or we can connect 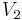 and
and 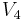 with a path containing vertices colored only with colors 2 and 4. The latter possibility is clearly absurd, as such a path would intersect the path we constructed in
with a path containing vertices colored only with colors 2 and 4. The latter possibility is clearly absurd, as such a path would intersect the path we constructed in 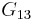 .
.
So  can in fact be five-colored, contrary to the initial presumption.
can in fact be five-colored, contrary to the initial presumption.
Linear time five-coloring algorithm
In 1996, Robertson, Sanders, Seymour, and Thomas described a quadratic four-coloring algorithm in their "Efficiently four-coloring planar graphs".[1] In the same paper they briefly describe a linear-time five-coloring algorithm, which is asymptotically optimal. The algorithm as described here operates on multigraphs and relies on the ability to have multiple copies of edges between a single pair of vertices. It is based on Wernicke's theorem, which states the following:
- Wernicke's Theorem: Assume G is planar, nonempty, has no faces bounded by two edges, and has minimum degree 5. Then G has a vertex of degree 5 which is adjacent to a vertex of degree at most 6.
We will use a representation of the graph in which each vertex maintains a circular linked list of adjacent vertices, in clockwise planar order.
In concept, the algorithm is recursive, reducing the graph to a smaller graph with one less vertex, five-coloring that graph, and then using that coloring to determine a coloring for the larger graph in constant time. In practice, rather than maintain an explicit graph representation for each reduced graph, we will remove vertices from the graph as we go, adding them to a stack, then color them as we pop them back off the stack at the end. We will maintain three stacks:
- S4: Contains all remaining vertices with either degree at most four, or degree five and at most four distinct adjacent vertices (due to multiple edges).
- S5: Contains all remaining vertices that have degree five, five distinct adjacent vertices, and at least one adjacent vertex with degree at most six.
- Sd: Contains all vertices deleted from the graph so far, in the order that they were deleted.
The algorithm works as follows:
- In the first step, we collapse all multiple edges to single edges, so that the graph is simple. Next, we iterate over the vertices of the graph, pushing any vertex matching the conditions for S4 or S5 onto the appropriate stack.
- Next, as long as S4 is non-empty, we pop v from S4 and delete v from the graph, pushing it onto Sd, along with a list of its neighbors at this point in time. We check each former neighbor of v, pushing it onto S4 or S5 if it now meets the necessary conditions.
- When S4 becomes empty, we know that our graph has minimum degree five. If the graph is empty, we go to the final step 5 below. Otherwise, Wernicke's Theorem tells us that S5 is nonempty. Pop v off S5, delete it from the graph, and let v1, v2, v3, v4, v5 be the former neighbors of v in clockwise planar order, where v1 is the neighbor of degree at most 6. We check if v1 is adjacent to v3 (which we can do in constant time due to the degree of v1). There are two cases:
- If v1 is not adjacent to v3, we can merge these two vertices into a single vertex. To do this, we remove v from both circular adjacency lists, and then splice the two lists together into one list at the point where v was formerly found. Provided that v maintains a reference to its position in each list, this can be done in constant time. It's possible that this might create faces bounded by two edges at the two points where the lists are spliced together; we delete one edge from any such faces.
After doing this, we push v3 onto Sd, along with a note that v1 is the vertex that it was merged with. Any vertices affected by the merge are added or removed from the stacks as appropriate.
- Otherwise, v2 lies inside the face outlined by v, v1, and v3. Consequently, v2 cannot be adjacent to v4, which lies outside this face. We merge v2 and v4 in the same manner as v1 and v3 above.
- If v1 is not adjacent to v3, we can merge these two vertices into a single vertex. To do this, we remove v from both circular adjacency lists, and then splice the two lists together into one list at the point where v was formerly found. Provided that v maintains a reference to its position in each list, this can be done in constant time. It's possible that this might create faces bounded by two edges at the two points where the lists are spliced together; we delete one edge from any such faces.
- Go to step 2.
- At this point S4, S5, and the graph are empty. We pop vertices off Sd. If the vertex was merged with another vertex in step 3, the vertex that it was merged with will already have been colored, and we assign it the same color. This is valid because we only merged vertices that were not adjacent in the original graph. If we had removed it in step 2 because it had at most 4 adjacent vertices, all of its neighbors at the time of its removal will have already been colored, and we can simply assign it a color that none of its neighbors is using.
See also
References
Further reading
- Heawood, P. J. (1890), "Map-Colour Theorems", Quarterly Journal of Mathematics, Oxford 24: 332–338